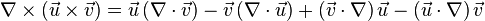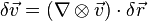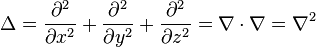1. IDL Routines Syntax
Refer to : http://www.physics.nyu.edu/grierlab/idl_html_help/idl_alph.html
2. IDL Statement Syntax
Refer to : https://www.astro.virginia.edu/class/oconnell/astr511/IDLresources/idl-syntx-sterner.html
Index
DefinitionsAssignment
If
For
While
Repeat
Case
Goto
Block
Common
Procedure
Function
Some definitions
- Operators: Items like +,-,*,/ and so on.
- Constants: Items like 3, [3,2,5], "A string", AND, OR, and so on.
- Variables: A named item used to store a value.
- Expression: A constant, variable, or set of constants and/or variables combined by operators.
- Statement: A single IDL statement or a statement block (see below).
- Routine: A procedure or a function.
Assignment
- Purpose: place a value in a variable.
- Syntax: Variable = expression
- Examples:
- x = 7
- num = [12,32,52,12]
- y = 3*x^2 + 7*x - 5
- cat = dog
- Notes: expression may be a constant, variable, or combination of terms and operators
If
- Purpose: Conditionally execute a statement.
- Syntax:
if expression then statement
if expression then statement1 else statement2 - Examples:
- if y lt 0 then t=2
- if y lt 0 then t=2 else t=3
if y lt 0 then begin t=2 txt='Negative' endifif y lt 0 then begin t=2 txt='Negative' endif else begin t=3 txt='Non-negative' endelse- if ((x gt -2) and (x lt 3)) and ((y gt 5) and (y lt 8)) then t=2
- Notes: For complicated expressions parentheses may be used to make sure expression has the desired meaning.
For Loops
- Purpose: Repeat a statement a specified number of times.
- Syntax: for variable = init, limit, step do statement
- Examples:
- for i=0,9 do print,i
- for t=1.0, 0.01, -.01 do plots,x*t,y*t
for ix=0L, n, 10 do begin x(j) = xx(ix) j = j+1 print,ix endfor
- Notes: The loop variable has the same data type as the initial value (init above). Make sure to use the correct data type for the initial value. A common error is: for t=0,1,.1 do ... which gives an infinite loop since .1 added to an integer variable does nothing. This is easily fixed: t=0.,1,.1 (note the 0. instead of 0). Another common error is not forcing a loop variable to be a long integer when the loop can go above 32767. The fix is: for i=0L,... A for loop may be executed 0 times if the loop variable starts beyond the loop limit.
While Loops
- Purpose: Repeat a statement while some condition is true.
- Syntax: while expression do statement
- Examples:
- while x gt 0 do x=x-1
while not eof(lun) do begin readf,lun,txt print,txt endwhile
- Notes: A while statement may be executed 0 or more times depending on the value of the expression.
Repeat Loops
- Purpose: Repeat a statement until some condition is true.
- Syntax: repeat statement until expression
- Examples:
- repeat x=x-1 until x le 0
repeat begin readf, lun, x x = x-c endrep until x le 0
- Notes: A repeat statement is always executed at least once.
Case
- Purpose: Selectively execute a statement based on the value of an expression.
- Syntax:
case expression of expression: statement . . . expression: statement else: statement endcase - Examples:
case animal of 'cat': print,'meow' 'dog': print,'arf arf' 'bird': print,'tweet tweet' else: print,'??' endcasecase t>0<2 of 0: begin txt = 'red' err = 0 end 1: begin txt = 'green' err = 0 end 2: begin txt = 'blue' err = 1 end endcase
- Notes: The expression following the word case is compared to a list of expressions. The statement corresponding to the first match is executed. If no match is found the statement following the else is executed. Else is optional but if no match is found and else is not included an error will result.
Goto
- Purpose: Jump to a specified label in a routine.
- Syntax: goto, label
- Examples:
. . . loop: . . . goto, loop. . . goto, err . . . err: print,' Error ...' . . .
- Notes: May only be used in routines. Program flow jumps to the specified label. If label does not occur in the routine a compile error results.
Blocks
- Purpose: Allows multiple statements to be executed anywhere a single statement is allowed.
- Syntax:
begin statement 1 . . . statement n end - Examples:
- if x lt 0 then begin print,x & a=2 & endif
- for i=0, 10 do begin readf, lun, txt & print,txt & endfor
- Notes: The plain end statement may be replaced by a more specific end statement for the following cases: if, else, for, while, and repeat. The corresponding end statements are: endif, endelse, endfor, endwhile, and endrep. While not enforced, these should always be used so the compiler can do better error checking. Only the case statement uses the plain begin/end pair to execute multiple statements for a match (the endcase is not really one of the end statements).
Common
- Purpose: Share variables between routines or remember values between calls to a routine.
- Syntax: common name, variable_1, variable_2, . . . variable_n, name is the name of the common block. Variables are matched by position so need not have the same name in each routine.
- Examples:
- common xkodak_com, x, y, dx, dy, file, count
- common random_plot_com, seed
- Notes: A single routine may use a common to save the value of
a variable between calls. Some examples of where this is useful:
to remember default values, to remember a seed value for the randomu (or
randomn) function since the system clock is used if no seed is given and
for fast computers the same seed may be used for several calls.
Several routines may use a common to share status values. In such cases
it is useful to store the common in a separate file and include it in
each routine (@filename where @ is in column 1). This way only a single
copy of the common need be maintained.
A good way to name commons is to use the main routine name followed by _com, like xkodak_com. This helps prevent the accidental use of the same name for diffrent commons.
Procedure definition
- Purpose: Specify a procedure name and parameters.
- Syntax: pro name, parameter_1, parameter_2, ... parameter_n name is the name of the procedure.
- Examples:
- pro test, a, b, c
- pro compute, x, y, z, flag=flg, help=hlp
- Notes: A procedure must end with an end statement and
may have one or more return statements inside.
If program flow reaches the final end statement a return is implied.
Example calls to the above procedures:
test, 2, 3, out
compute, x, y, z, /flag
Function definition
- Purpose: Specify a function name and parameters.
- Syntax: function name, parameter_1, parameter_2, ... parameter_n name is the name of the function.
- Examples:
- function test, a, b, c
- function compute, x, y, z, flag=flg, help=hlp
- Notes: A function must end with an end statement and
must have one or more return statements inside.
A return statement in a function must include the return value:
return, value.
Example calls to the above procedures:
a = test(2, 3, 5)
t = compute(x, y, z, /flag)
and 
, del is defined in terms of 
and standard basis 
, del is written as
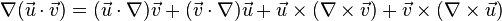
is a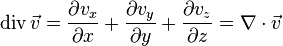 
is defined as:
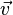is a 9-term second-rank tensor, but can be denoted simply as 
, where 
represents the 
, the change in the vector field is given by:
)
)
)
