Friday, September 5, 2014

nabla ∇

Del, or nabla, is an operator used in mathematics, in particular, in vector calculus, as a vector differential operator, usually represented by the nabla symbol ∇.


In the Cartesian coordinate system Rn with coordinates (x_1, \dots, x_n) and standard basis \{ \mathbf{\hat e}_1, \dots, \mathbf{\hat e}_n \}, del is defined in terms of partial derivative operators as
\nabla = \left( {\partial \over \partial x_1}, \cdots, {\partial \over \partial x_n} \right) = \sum_{i=1}^n \mathbf{\hat e}_i {\partial \over \partial x_i}
In three-dimensional Cartesian coordinate system R3 with coordinates (x, y, z) and standard basis \{ \mathbf{\hat{x}}, \mathbf{\hat{y}}, \mathbf{\hat{z}} \}, del is written as
\nabla = \left( {\partial \over \partial x}, {\partial \over \partial y}, {\partial \over \partial z} \right) = \mathbf{\hat{x}} {\partial \over \partial x} + \mathbf{\hat{y}} {\partial \over \partial y} + \mathbf{\hat{z}} {\partial \over \partial z}

Notational uses

Gradient

The vector derivative of a scalar field f is called the gradient, and it can be represented as:
\nabla f = {\partial f \over \partial x} \mathbf{\hat{x}} + {\partial f \over \partial y} \mathbf{\hat{y}} + {\partial f \over \partial z} \mathbf{\hat{z}}

 

In particular, this notation is powerful because the gradient product rule looks very similar to the 1d-derivative case:
\nabla(f g) = f \nabla g + g \nabla f
However, the rules for dot products do not turn out to be simple, as illustrated by:
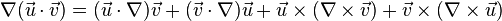
\nabla (\vec u \cdot \vec v) = (\vec u \cdot \nabla) \vec v + (\vec v \cdot \nabla) \vec u + \vec u \times (\nabla \times \vec v) + \vec v \times (\nabla \times \vec u)

 Divergence

The divergence of a vector field \vec{v}(x, y, z) = v_x \mathbf{\hat{x}} + v_y \mathbf{\hat{y}} + v_z \mathbf{\hat{z}} is a scalar function that can be represented as:
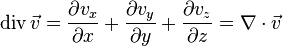
\mbox{div}\,\vec v = {\partial v_x \over \partial x} + {\partial v_y \over \partial y} + {\partial v_z \over \partial z} = \nabla \cdot \vec v  
 
 
The power of the del notation is shown by the following product rule:
\nabla \cdot (f \vec v) = f (\nabla \cdot \vec v) + \vec v \cdot (\nabla f)
The formula for the vector product is slightly less intuitive, because this product is not commutative:
\nabla \cdot (\vec u \times \vec v) = \vec v \cdot (\nabla \times \vec u) - \vec u \cdot (\nabla \times \vec v)

Curl

The curl of a vector field \vec{v}(x, y, z) = v_x\mathbf{\hat{x}} + v_y\mathbf{\hat{y}} + v_z\mathbf{\hat{z}} is a vector function that can be represented as:
\mbox{curl}\;\vec v = \left( {\partial v_z \over \partial y} - {\partial v_y \over \partial z} \right) \mathbf{\hat{x}} + \left( {\partial v_x \over \partial z} - {\partial v_z \over \partial x} \right) \mathbf{\hat{y}} + \left( {\partial v_y \over \partial x} - {\partial v_x \over \partial y} \right) \mathbf{\hat{z}} = \nabla \times \vec v

Directional derivative

The directional derivative of a scalar field f(x,y,z) in the direction \vec{a}(x,y,z) = a_x \mathbf{\hat{x}} + a_y \mathbf{\hat{y}} + a_z \mathbf{\hat{z}} is defined as:

Laplacian

The Laplace operator is a scalar operator that can be applied to either vector or scalar fields; for cartesian coordinate systems it is defined as:

Tensor derivative

Del can also be applied to a vector field with the result being a tensor. The tensor derivative of a vector field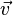 \vec{v} is a 9-term second-rank tensor, but can be denoted simply as 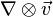\nabla \otimes \vec{v}, where \otimes represents the dyadic product. This quantity is equivalent to the transpose of the Jacobian matrix of the vector field with respect to space.
For a small displacement \delta \vec{r}, the change in the vector field is given by:

Product rules

\nabla (fg) = f\nabla g + g\nabla f
\nabla(\vec u \cdot \vec v) = \vec u \times (\nabla \times \vec v) + \vec v \times (\nabla \times \vec u) + ( \vec u \cdot \nabla) \vec v + (\vec v \cdot \nabla )\vec u
\nabla \cdot (f \vec v) = f (\nabla \cdot \vec v) + \vec v \cdot (\nabla f)
\nabla \cdot (\vec u \times \vec v) = \vec v \cdot (\nabla \times \vec u) - \vec u \cdot (\nabla \times \vec v )
\nabla \times (f \vec v) = (\nabla f) \times \vec v + f (\nabla \times \vec v)
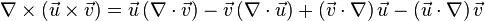
\nabla \times (\vec u \times \vec v) = \vec u \, (\nabla \cdot \vec v) - \vec v \, (\nabla \cdot \vec u) + (\vec v \cdot \nabla) \, \vec u - (\vec u \cdot \nabla) \, \vec v
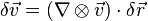
\delta \vec{v} = (\nabla \otimes \vec{v}) \sdot \delta \vec{r}
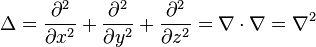
\Delta = {\partial^2 \over \partial x^2} + {\partial^2 \over \partial y^2} + {\partial^2 \over \partial z^2} = \nabla \cdot \nabla = \nabla^2
\vec{a}\cdot\mbox{grad}\,f = a_x {\partial f \over \partial x} + a_y {\partial f \over \partial y} + a_z {\partial f \over \partial z} = (\vec a \cdot \nabla) f
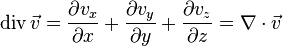
\mbox{div}\,\vec v = {\partial v_x \over \partial x} + {\partial v_y \over \partial y} + {\partial v_z \over \partial z} = \nabla \cdot \vec v
Posted by at
Labels:

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)